- Research
- Open access
- Published:
The acquisition of problem solving competence: evidence from 41 countries that math and science education matters
Large-scale Assessments in Education volume 2, Article number: 10 (2014)
Abstract
Background
On the basis of a ‘problem solving as an educational outcome’ point of view, we analyse the contribution of math and science competence to analytical problem-solving competence and link the acquisition of problem solving competence to the coherence between math and science education. We propose the concept of math-science coherence and explore whether society-, curriculum-, and school-related factors confound with its relation to problem solving.
Methods
By using the PISA 2003 data set of 41 countries, we apply multilevel regression and confounder analyses to investigate these effects for each country.
Results
Our results show that (1) math and science competence significantly contribute to problem solving across countries; (2) math-science coherence is significantly related to problem solving competence; (3) country-specific characteristics confound this relation; (4) math-science coherence is linked to capability under-utilisation based on science performance but less on math performance.
Conclusions
In sum, low problem solving scores seem a result of an impeded transfer of subjectspecific knowledge and skills (i.e., under-utilisation of science capabilities in the acquisition of problem solving competence), which is characterised by low levels of math-science coherence.
Background
The ability to solve real-world problems and to transfer problem-solving strategies from domain-specific to domain-general contexts and vice versa has been regarded an important competence students should develop during their education in school (Greiff et al. [2013]; van Merriënboer [2013]). In the context of large-scale assessments such as the PISA study problem solving competence is defined as the ability to solve cross-disciplinary and real-world problems by applying cognitive skills such as reasoning and logical thinking (Jonassen [2011]; OECD [2004]). Since this competence is regarded a desirable educational outcome, especially math and science educators have focused on developing students’ problem solving and reasoning competence in their respective domain-specific contexts (e.g., Kind [2013]; Kuo et al. [2013]; Wu and Adams [2006]). Accordingly, different conceptual frameworks were proposed that describe the cognitive processes of problem solving such as understanding the problem, building adequate representations of the problem, developing hypotheses, conducting experiments, and evaluating the solution (Jonassen [2011]; OECD [2005]). In comparing these approaches in math and science, it seems apparent that there is a conceptual overlap between the problem solving models in these two domains. This overlap triggers the question regarding its contribution to the development of students’ cross-curricular problem-solving competence (Abd-El-Khalick et al. [2004]; Bassok and Holyoak [1993]; Hiebert et al. [1996]).
The operationalization and scaling of performance in PISA assessments enables direct contrasting of scores in students’ competences in math and problem solving. Leutner et al. ([2012]) suggest that discrepancies between math and problem solving scores are indicative of the relative effectiveness of math education (OECD [2004]). In line with a “Capability-Utilisation Hypothesis”, it is assumed that math scores that negatively deviate from their problem solving counterpart signify an under-utilisation of students’ problem-solving capabilities as indicated by their scores in generic problem solving.
We intend to extend this view in two ways: First, by introducing the concept of math-science coherence we draw the focus on the potential synergistic link between math and science education and its contribution to the acquisition of problem solving competence. Second, the introduction of a Capability Under-Utilisation Index will enable us to extend the focus of the Capability-Utilisation Hypothesis to both, math and science education. The combination of the concept of math-science coherence with the notion of capability-utilisation will help to further explore the facilitating processes involved in the transition of subject-specific knowledge and skills to the acquisition of problem solving competence. These insights are expected to contribute to a better understanding of meaningful strategies to improve and optimize educational systems in different countries.
Theoretical framework
Problem solving as an educational goal
In the PISA 2003 framework, problem solving is referred to as “an individual’s capacity to use cognitive processes to resolve real, cross-disciplinary situations where the solution path is not immediately obvious” (OECD [2004], p. 156). This definition is based on the assumption of domain-general skills and strategies that can be employed in various situations and contexts. These skills and strategies involve cognitive processes such as: Understanding and characterizing the problem, representing the problem, solving the problem, reflecting and communicating the problem solution (OECD [2003]). Problem solving is often regarded a process rather than an educational outcome, particularly in research on the assessment and instruction of problem solving (e.g., Greiff et al. [2013]; Jonassen [2011]). This understanding of the construct is based on the assumption that problem solvers need to perform an adaptive sequence of cognitive steps in order to solve a specific problem (Jonassen [2011]). Although problem solving has also been regarded as a process skill in large-scale assessments such as the PISA 2003 study, these assessments mainly focus on problem solving performance as an outcome that can be used for international comparisons (OECD [2004]). However, problem solving competence was operationalized as a construct comprised of cognitive processes. In the context of the PISA 2003 study, these processes were referred to as analytical problem solving, which was assessed by static tasks presented in paper-and-pencil format. Analytical problem-solving competence is related to school achievement and the development of higher-order thinking skills (e.g., Baumert et al. [2009]; OECD [2004]; Zohar [2013]). Accordingly, teachers and educators have focused on models of problem solving as guidelines for structuring inquiry-based processes in their subject lessons (Oser and Baeriswyl [2001]). Van Merriënboer ([2013]) pointed out that problem solving should not only be regarded a mere instructional method but also as a major educational goal. Recent curricular reforms have therefore shifted towards the development of problem solving abilities in school (Gallagher et al. [2012]; Koeppen et al. [2008]). These reforms were coupled with attempts to strengthen the development of transferable skills that can be applied in real-life contexts (Pellegrino and Hilton [2012]). For instance, in the context of 21st century skills, researchers and policy makers have agreed on putting emphasis on fostering skills such as critical thinking, digital competence, and problem solving (e.g., Griffin et al. [2012]). In light of the growing importance of lifelong learning and the increased complexity of work- and real-life problem situations, these skills are now regarded as essential (Griffin et al. [2012]; OECD [2004]). Hence, large-scale educational studies such as PISA have shifted towards the assessment and evaluation of problem solving competence as a 21st century skill.
The PISA frameworks of math and science competence
In large-scale assessments such as the PISA studies, students’ achievement in the domains of science and mathematics play an important role. Moreover, scientific and mathematical literacy are now regarded essential to being a reflective citizen (Bybee [2004]; OECD [2003]). Generally, Baumert et al. ([2009]) have shown that students’ math and science achievements are highly related to domain-general ability constructs such as reasoning or intelligence. In this context, student achievement refers to “the result of domain-specific processes of knowledge acquisition and information processing” (cf. Baumert et al. [2009], p. 169). This line of argument is reflected in definitions and frameworks of scientific and mathematical literacy, which are conceptualized as domain-specific competences that are hierarchically organized and build upon abilities closely related to problem solving (Brunner et al. [2013]).
Scientific literacy has been defined within a multidimensional framework, differentiating between three main cognitive processes, namely describing, explaining, and predicting scientific phenomena, understanding scientific investigations, and interpreting scientific evidence and conclusions (OECD [2003]). In addition, various types of knowledge such as ‘knowledge about the nature of science’ are considered as factors influencing students’ achievements in this domain (Kind [2013]). We conclude that the concept of scientific literacy encompasses domain-general problem-solving processes, elements of scientific inquiry (Abd-El-Khalick et al. [2004]; Nentwig et al. [2009]), and domain-specific knowledge.
The definition of mathematical literacy refers to students’ competence to utilise mathematical modelling and mathematics in problem-solving situations (OECD [2003]). Here, we can also identify overlaps between cognitive processes involved in mathematical problem solving and problem solving in general: Structuring, mathematizing, processing, interpreting, and validating (Baumert et al. [2009]; Hiebert et al. [1996]; Kuo et al. [2013]; Polya [1945]). In short, mathematical literacy goes beyond computational skills (Hickendorff [2013]; Wu and Adams [2006]) and is conceptually linked to problem solving.
In the PISA 2003 framework, the three constructs of math, science, and problem solving competence overlap conceptually. For instance, solving the math items requires reasoning, which comprises analytical skills and information processing. Given the different dimensions of the scientific literacy framework, the abilities involved in solving the science items are also related to problem solving, since they refer to the application of knowledge and the performance of inquiry processes (OECD [2003]). This conceptual overlap is empirically supported by high correlations between math and problem solving (r = .89) and between science and problem solving (r = .80) obtained for the sample of 41 countries involved in PISA 2003 (OECD [2004]). The relation between math and science competence was also high (r = .83). On the one hand, the sizes of the inter-relationships, give rise to the question regarding the uniqueness of each of the competence measures. On the other hand, the high correlations indicate that problem-solving skills are relevant in math and science (Martin et al. [2012]). Although Baumert et al. ([2009]) suggest that the domain-specific competences in math and science require skills beyond problem solving (e.g., the application of domain-specific knowledge) we argue from an assessment perspective that the PISA 2003 tests in math, science, and problem solving measure predominantly basic academic skills relatively independent from academic knowledge (see also Bulle [2011]).
The concept of capability-utilisation
Discrepancies between students’ performance in math/science and problem solving were studied at country level (OECD [2004]) and were, for example for math and problem solving scores, interpreted in two ways: (1) If students’ perform better in math than in problem solving, they would “have a better grasp of mathematics content […] after accounting for the level of generic problem-solving skills…” (OECD [2004], p. 55); (2) If students’ estimated problem-solving competence is higher than their estimated math competence, “… this may suggest that students have the potential to achieve better results in mathematics than that reflected in their current performance…” (OECD [2004], p. 55). Whilst the latter discrepancy constitutes a capability under-utilisation in math, the former suggests challenges in utilising knowledge and skills acquired in domain-specific contexts in domain-unspecific contexts (i.e., transfer problem).
To quantify the degree to which students are able to transfer their problem solving capabilities from domain-specific problems in math or science to cross-curricular problems, we introduce the Capability Under-Utilisation Index (CUUI) as the relative difference between math or science and problem solving scores:
and
A positive CUUI indicates that the subject-specific education (i.e., math or science) in a country tends to under-utilise its students’ capabilities to problem solve. A negative CUUI indicates that a country’s educational system fails to fully utilise its students’ capabilities to acquire math and science literacy in the development of problem solving. The CUUI reflects the relative discrepancies between the achievement scores in different domainsa.
The concept of math-science coherence
In light of the conceptual and empirical discussion on the relationship between math, science, and problem solving competence, we introduce the concept of math-science coherence as follows: First, math-science coherence refers to the set of cognitive processes involved in both subjects and thus represents processes which are related to reasoning and information processing, relatively independent from domain-specific knowledge. Second, math-science coherence reflects the degree to which math and science education is harmonized as a feature of the educational environment in a country. This interpretation is based on the premise that PISA measures students’ competence as educational outcomes (OECD [2004]). The operationalization of math-science coherence is realized by means of the correlation between math and science scores [r(M,S)] at the country level. Low math-science coherence indicates that students who are successful in the acquisition of knowledge and skills in math are not necessarily successful in the acquisition of knowledge and skills in science and vice versa.
On the basis of this conceptualization of math-science coherence, we expect a significant and positive relation to problem solving scores, since the conceptual overlap between mathematical and scientific literacy refers to cognitive abilities such as reasoning and information processing that are also required in problem solving (Arts et al. [2006]; Beckmann [2001]; Wüstenberg et al. [2012]). Hence, we assert that math-science coherence facilitates the transfer of knowledge, skills, and insights across subjects resulting in better problem solving performance (OECD [2004]; Pellegrino and Hilton [2012]).
We also assume that math-science coherence as well as capability utilisation is linked to characteristics of the educational system of a country. For instance, as Janssen and Geiser ([2012]) and Blömeke et al. ([2011]) suggested, the developmental status of a country, measured by the Human Development Index (HDI; UNDP [2005]), is positively related to students’ academic achievements as well as to teachers’ quality of teaching. Furthermore, the socio-economic status of a country co-determines characteristics of its educational system, which ultimately affects a construct referred to as national intelligence (Lynn and Meisenberg [2010]). Research also indicated that curricular settings and educational objectives are related to school achievement in general (Bulle [2011]; Martin et al. [2004]). Besides these factors, school- and classroom-related characteristics might also confound the relation between math-science coherence and problem solving. For instance, the schools’ autonomy in developing curricula and managing educational resources might facilitate the incorporation of inquiry- and problem-based activities in science lessons (Chiu and Chow [2011]). These factors have been discussed as being influential to students’ competence development (OECD [2004], [2005]). Ewell ([2012]) implies that cross-national differences in problem solving competence might be related to differences in education and in using appropriate teaching material. These factors potentially confound the relation between math-science coherence and problem solving.
Discrepancies between math and problem solving scores are discussed in relation to quality of education. Although research has found that crossing the borders between STEM subjects positively affects students’ STEM competences (e.g., National Research Council NRC [2011]), we argue that the PISA analyses have fallen short in explaining cross-country differences in the development of problem solving competence, since they ignored the link between math and science competences and the synergistic effect of learning universally applicable problem-solving skills in diverse subject areas. Hence, we use the concept of math-science coherence to provide a more detailed description of the discrepancies between problem solving and domain-specific competences. In this regard, we argue that the coherence concept indicates the synergistic potential and students’ problem-solving competence the success of transfer.
The present study
The current study is based on the premise that in contrast to math and science competence problem solving competence is not explicitly taught as a subject at school. Problem solving competence, however, is an expected outcome of education (van Merriënboer [2013]). With the first step in our analyses, we seek to establish whether math and science education are in fact main contributors to the acquisition of problem solving competence. On the basis of this regression hypothesis, we subsequently focus on the question whether there are significant and systematic differences between countries (Moderation-Hypothesis). In light of the conceptual overlap due to cognitive processes involved in dealing with math, science and problem solving tasks and the shared item format employed in the assessments, we expect math and science competence scores to substantially predict scores in problem solving competence. Furthermore, since math and science education are differently organized across the 41 countries participating in the PISA 2003 study, differences in the contribution are also expected.
On the basis of these premises, we introduce the concept of math-science coherence, operationalised as the correlation between math and science scores [r(M,S)], and analyse its relationship to problem solving and the effects of confounders (i.e., country characteristics) as a step of validation. Since math, science, and problem solving competence show a conceptual overlap, we expect problem solving and math-science coherence to be positively related. Countries’ educational systems differ in numerous aspects, their educational structure, and their educational objectives. Countries also differ with regard to the frequency of assessments, the autonomy of schools in setting up curricula and resources, and the educational resources available. Consequently, we expect the relation between math-science coherence and problem solving competence to be confounded by society-, curriculum-, and school-related factors (Confounding-Hypothesis).
In a final step, we aim to better understand the mechanisms with which math and science education contributes to the acquisition of problem-solving competence by exploring how math-science coherence, capability utilisation, and problem solving competence are related. We thus provide new insights into factors related to the transfer between students’ domain-specific and cross-curricular knowledge and skills (Capability-Utilisation Hypothesis).
Methods
Sample
In PISA 2003, a total sample of N = 276,165 students (49.4% female) from 41 countries participated. The entire sample was randomly selected by applying a two-step sampling procedure: First, schools were chosen within a country. Second, students were chosen within these schools. This procedure consequently led to a clustered structure of the data set, as students were nested in 10,175 schools. On average, 27 students per school were chosen across schools within countries. Students’ mean age was 15.80 years (SD = 0.29 years) ranging from 15.17 to 16.25 years.
Measures
In the PISA 2003 study, different assessments were used in order to measure students’ competence in math, science, and problem solving. These assessments were administered as paper-and-pencil tests within a multi-matrix design (OECD [2005]). In this section, the assessments and further constructs are described that served as predictors of the contribution of math and science competence to problem solving at the country level.
Student achievement in math, science, and problem solving
In order to assess students’ competence to solve cross-curricular problems (i.e., analytical problem solving requiring information retrieval and reasoning), students had to work on an analytical problem-solving test. This test comprised a total of 19 items (7 items referred to trouble-shooting, 7 items referred to decision-making, and 5 items referred to system analysis and design; see OECD [2004]). Items were coded according to the PISA coding scheme, resulting in dichotomous and polytomous scores (OECD [2005]). Based on these scores, models of item response theory were specified in order to obtain person and item parameters (Leutner et al. [2012]). The resulting plausible values could be regarded as valid indicators of students’ abilities in problem solving (Wu [2005]). The problem solving test showed sufficient reliabilities between .71 and .89 for the 41 countries.
To assess mathematical literacy as an indicator of math competence, an 85-items test was administered (for details, refer to OECD [2003]). Responses were dichotomously or polytomously scored. Again, plausible values were obtained as person ability estimates and reliabilities were good (range: 0.83 – 0.93). In the context of mathematical literacy, students were asked to solve real-world problems by applying appropriate mathematical models. They were prompted to “identify and understand the role mathematics plays in the world, to make well-founded judgements and to use […] mathematics […]” (OECD [2003], p. 24).
Scientific literacy as a proxy for science competence was assessed by using problems referring to different content areas of science in life, health, and technology. The reliability estimates for the 35 items in this test ranged between .68 and .88. Again, plausible values served as indicators of this competence.
Country-specific characteristics
In our analyses, we incorporated a range of country-specific characteristics that can be subdivided into three main categories. These are: society-related factors, curriculum-related factors, and school-related factors. Country-specific estimates of National Intelligence as derived by Lynn and Meisenberg ([2010]) as well as the Human Development Index (HDI) were subsumed under society-related factors. The HDI incorporates indicators of a country’s health, education, and living standards (UNDP [2005]). Both variables are conceptualised as factors that contribute to country-specific differences in academic performance.
Holliday and Holliday ([2003]) emphasised the role of curricular differences in the understanding of between-country variance in test scores. We incorporated two curriculum-related factors in our analyses. First, we used Bulle’s ([2011]) classification of curricula into ‘progressive’ and ‘academic’. Bulle ([2011]) proposed this framework and classified the PISA 2003 countries according to their educational model. In her framework, she distinguishes between ‘academic models’ which are primarily geared towards teaching academic subjects (e.g., Latin, Germanic, and East-Asian countries) and ‘progressive models’ which focus on teaching students’ general competence in diverse contexts (e.g., Anglo-Saxon and Northern countries). In this regard, academic skills refer to the abilities of solving academic-type problems, whereas so called progressive skills are needed in solving real-life problems (Bulle [2011]). It can be assumed that educational systems that focus on fostering real-life and domain-general competence might be more conducive to successfully tackling the kind of problem solving tasks used in PISA (Kind [2013]). This classification of educational systems should be seen as the two extreme poles of a continuum rather than as a strict dichotomy. In line with the reflections above, we would argue that academic and progressive skills are not exclusively distinct, since both skills utilise sets of cognitive processes that largely overlap (Klahr and Dunbar [1988]). The fact that curricular objectives in some countries are shifting (e.g., in Eastern Asia) makes a clear distinction between both models even more difficult. Nonetheless, we will use this form of country-specific categorization based on Bulle’s model in our analyses.
Second, we considered whether countries’ science curricula were ‘integrated’ or ‘not integrated’ (Martin et al. [2004]). In this context, integration refers to linking multiple science subjects (biology, chemistry, earth science, and physics) to a unifying theme or issue (cf. Drake and Reid [2010], p. 1).
In terms of school-related factors, we used the PISA 2003 scales of ‘Frequency of assessments in schools’, ‘Schools’ educational resources’, and ‘School autonomy towards resources and curricula’ from the school questionnaire. Based on frequency and rating scales, weighted maximum likelihood estimates (WLE) indicated the degree to which schools performed in these scales (OECD [2005]).
The country-specific characteristics are summarized in the Table 1.
Procedure
The PISA 2003 assessments utilised a randomized incomplete block design to select different test booklets which covered the different content areas of math, science, and problem solving (Brunner et al. [2013]; OECD [2005]). The test administration took 120 minutes, and was managed for each participating country separately. It was established that quality standards of the assessment procedure were high.
Statistical analyses
In PISA 2003, different methods of obtaining person estimates with precise standard errors were applied. The most accurate procedure produced five plausible values, which were drawn from a person ability distribution (OECD [2005]). To avoid missing values in these parameters and to obtain accurate estimates, further background variables were used within the algorithms (Wu [2005]). The resulting plausible values were subsequently used as indicators of students’ competence in math, science, and problem solving. By applying Rubin’s combination rules (Bouhilila and Sellaouti [2013]; Enders [2010]), analyses were replicated with each of the five plausible values and then combined. In this multiple imputation procedure, standard errors were decomposed to the variability across and within the five imputations (Enders [2010]; OECD [2005]; Wu [2005]).
Within the multilevel regression analyses for each country, we specified the student level as level 1 and the school level as level 2. Since PISA 2003 applied a random sampling procedure at the student and the school level, we decided to control for the clustering of data at these two levels (OECD [2005]). In addition to this two-level procedure, we regarded the 41 countries as multiple groups (fixed effects). This decision was based on our assumption that the countries selected in PISA 2003 did not necessarily represent a sample of a larger population (Martin et al. [2012]). Moreover, we did not regard the effects of countries as interchangeable, because, given the specific characteristics of education and instruction within countries; we argue that the effects of competences in mathematics and science on problem solving have their own distinct interpretation in each country (Snijders and Bosker [2012]). The resulting models were compared by taking into account the Akaike’s information criteria (AIC), Bayesian information criteria (BIC), and the sample-size adjusted BIC. Also, a likelihood ratio test of the log-Likelihood values (LogL) was applied (Hox [2010]).
To test the Moderation-Hypothesis, we first specified a two-level regression model with problem solving scores as outcomes at the student level (level 1), which allowed variance in achievement scores across schools (level 2). In this model, math and science scores predicted problem solving scores at the student level. To account for differences in the probabilities of being selected as a student within the 41 countries and to adjust the standard errors of regression parameters, we used the robust maximum likelihood (MLR) estimator and students’ final weights (see also Brunner et al. [2013]; OECD [2005]). All analyses were conducted in Mplus 6.0 by using the TYPE = IMPUTATION option (Muthén and Muthén [2010]). As Hox ([2010]) suggested, using multilevel regression models without taking into account the clustering of data in schools often leads to biased estimates, since achievement variables often have substantial variance at the school level. Consequently, we allowed for level-2-variance within the scores.
After having established whether success in math and science education contributes to the development in problem solving competence across the 41 countries, we then tested whether cross-country differences in the unstandardized regression coefficients were statistically significant by using a multi-group regression model, in which the coefficients were constrained to be equal across countries. We compared this model with the freely estimated model.
Finally, we conceptualized the correlation between math and science scores as an indicator of the level of coherence in math and science education in a country. In relation to the Confounding-Hypothesis, we tested country-specific characteristics for their potentially confounding effects on the relation between math-science coherence and problem solving competence. Following the recommendations proposed by (MacKinnon et al. [2000]), the confounding analysis was conducted in two steps: (1) we estimated two regression equations. In the first equation, problem solving scores across the 41 countries were regressed on math-science coherence. In the second equation, the respective country characteristics were added as further predictors; (2) the difference between the regression coefficients for math-science coherence obtained in either equation represented the magnitude of a potential confounder effect.
Lastly, we tested the Capability-Utilisation Hypothesis by investigating the bivariate correlations among the CUU Indices and math-science coherence.
Results
Regressing problem solving on math and science performance
To test the Moderation-Hypothesis, we specified regression models with students’ problem-solving score as the outcome and math and science scores as predictors for each of the 41 countries. Due to the clustering of data in schools, these models allowed for between-level variance. Intraclass correlations (ICC-1) for math, science, and problem solving performance ranged between .03 and .61 for the school level (M = .33, SD = .16).
We specified multilevel regression models for each country separately. These results are reported in Table 2. The regression coefficients for math on problem solving ranged from .53 to .82 with an average of M( βMath) = .67 (SD = .06). The average contribution of science towards problem solving was M( βScience) = .16 (SD = .09, Min = -.06, Max = .30). The combination of the distributions of both parameters resulted in substantial differences in the variance explanations of the problem solving scores across the 41 countries (M[R2] = .65, SD = .15, Min = .27, Max = .86). To test whether these differences were statistically significant, we constrained the regression coefficients of math and science competence within the multi-group regression model to be equal across the 41 countries. Compared to the freely estimated model (LogL = -4,561,273.3, df = 492, AIC = 9,123,530.5, BIC = 9,128,410.7), the restricted model was empirically not preferred LogL = -4,564,877.9, df = 412, AIC = 9,130,579.8, BIC = 9,134,917.6; Δχ2[80] = 7,209.2, p < .001. These findings lend evidence for the Moderation-Hypothesis.
From a slightly different perspective, the country-specific amount of variance in problem solving scores that is explained by the variation in math and science performance scores (R2) is strongly associated with the country’s problem solving score (r = .77, p < .001), which suggests that the contribution of science and math competence to the acquisition of problem solving competence was significantly lower in low-performing countries.
As shown in Table 2, the regression weights of math and science were significant for all but two countries. Across countries the regression weight for math tended to be higher than the regression weight for science when predicting problem solving competence. This finding indicates a stronger overlap between students’ competences in mathematics and problem solving on the one hand and similarities between the assessments in both domains on the other hand.
Validating the concept of math-science coherence
In order to validate the concept of math-science coherence, which is operationalised as the correlation between math and science scores [r(M,S)], we explored its relation to problem solving and country characteristics.
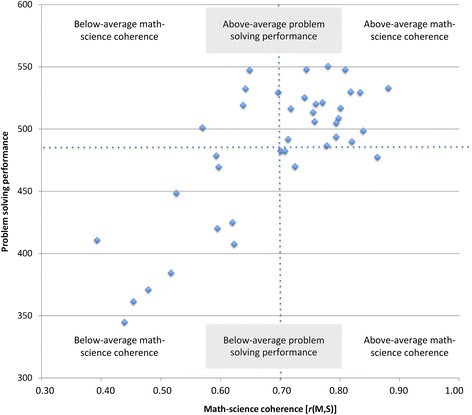
Regarding the regression outcomes shown in Table 2, it is apparent that math-science coherence varied considerably across countries, ranging from .39 to .88 with an average of M(r) = .70 (SD = .13). Interestingly, countries’ level of coherence in math-science education was substantially related to their problem solving scores (r = .76, p < .001). An inspection of Figure 1 reveals that this effect was mainly due to countries that both achieve low problem solving scores and show relatively low levels of math-science coherence (see bottom left quadrant in Figure 1), whilst amongst the remaining countries the correlational link between math-science coherence and problem solving score was almost zero (r = -.08, p = .71)b. This pattern extends the moderation perspective on the presumed dependency of problem solving competence from math and science competences.
As a result of the moderator analysis, we know that countries not only differ in regard to their average problem-solving scores and level of coherence between math and science, countries also differ in the strengths with which math-science coherence predicts problem solving scores. To better understand the conceptual nature of the link between math-science coherence and problem solving, we now attempt to adjust this relationship for potential confounding effects that country-specific characteristics might have. To this end, we employed linear regression and path analysis with students’ problem-solving scores as outcomes, math-science coherence (i.e., r[M,S]) as predictor, and country characteristics as potential confounders.
To establish whether any of the country characteristics had a confounding effect on the link between math-science coherence and problem solving competence, two criteria had to be met: (1) a reduction of the direct effect of math-science coherence on problem solving scores, and (2) testing the difference between the direct effect within the baseline Model M0 and the effect with the confounding Model M1 (Table 3).
Regarding the society-related factors, both the countries’ HDI and their national intelligence were confounders with a positive effect. Furthermore, the countries’ integration of the science curriculum was also positively related to the problem solving performance. Finally, the degree of schools’ autonomy towards educational resources and the implementation of curricula and the frequency of assessments were school-related confounders, the former with a positive effect whilst the latter represents a negative confounder. The direct effect of math-science coherence to problem solving decreased and thus indicated that confounding was present (MacKinnon et al. [2000]).
These findings provide evidence on the Confounding-Hypothesis and support our expectations on the relation between math-science coherence, problem solving, and country characteristics. We regard these results as evidence for the validity of the math-science coherence measure.
Relating math-science coherence to the capability under-utilisation indices
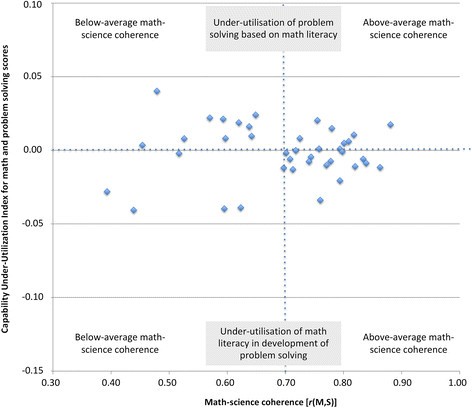
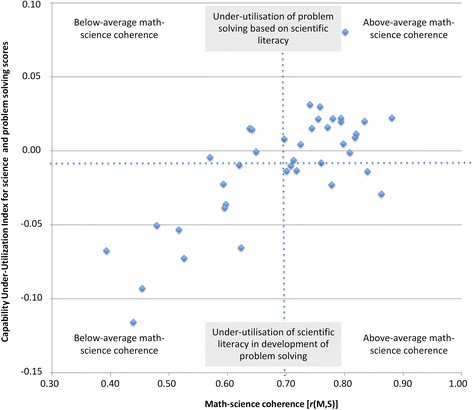
To advance our understanding of the link between math-science coherence and problem solving scores, we tested the Capability-Utilisation Hypothesis. To this end, we explored the relationship between math-science coherence and the CUU Indices for math and science, respectively. For math competence the average Capability Under-Utilisation Index was rather neutral with MCUUI-Math = -0.001 (SD = 0.02). This suggests that, on average, all countries sufficiently utilise their students’ math capabilities in facilitating the development of problem solving competence (i.e., transfer). It also suggests that math education across participating countries tends to sufficiently utilise generic problem-solving skills (Figure 2). The picture is different for science education. Here, the Capability Under-Utilisation Indices and their variation across the participating countries (MCUUI-Science = -0.01, SD = 0.04) suggest that in a range of countries knowledge and skills taught in science education tend to be under-utilised in the facilitation of the acquisition of problem solving competence (Figure 3).
For math competence, the relative difference to problem solving was not related to math-science coherence (r = .02, p = .89; Figure 2). In contrast, the Capability Under-Utilisation Index for science showed a strong positive correlation with math-science coherence (r = .76, p < .001; Figure 3), indicating that low levels of coherence between math and science education were associated with a less effective transfer of domain-specific knowledge and skills to problem solving.
Discussion
The present study was aimed at investigating the differences in the contribution of math and science competence to problem solving competence across the 41 countries that participated in the PISA 2003 study (Moderation-Hypothesis). To this end, we proposed the concept of math-science coherence and explored its relationship to problem solving competence and how this relationship is confounded by country characteristics (Confounding-Hypothesis). To further extend our understanding of the link between math-science coherence and problem solving, we introduced the concept of capability-utilisation. Testing the Capability-Utilisation Hypothesis enabled us to identify what may contribute to varying levels of math-science coherence and ultimately the development of problem solving competence.
The contribution of math and science competence across countries
Regarding the prediction of problem solving competence, we found that in most countries, math and science competence significantly contributed to students’ performance in analytical problem solving. This finding was expected based on the conceptualizations of mathematical and scientific literacy within the PISA framework referring to shared cognitive processes such as information processing and reasoning (Kind [2013]; OECD [2005]), which are regarded as components of problem solving (Bybee [2004]; Klahr and Dunbar [1988]; Mayer [2010]).
It is noteworthy that, for some of the below-average performing countries, science competence did not significantly contribute to the prediction of problem solving competence. It can be speculated that education in these countries is more geared towards math education and modelling processes in mathematical scenarios, whilst the aspect of problem solving in science is less emphasised (Janssen and Geiser [2012]). The results of multilevel regression analyses supported this interpretation by showing that math competence was a stronger predictor of problem solving competence. On the one hand, this finding could be due to the design of the PISA tests (Adams [2005]), since math and problem solving items are designed in such a way that modelling real-life problems is required, whereas science items are mostly domain-specific and linked to science knowledge (Nentwig et al. [2009]; OECD [2004]). Moreover, one may argue that math and problem solving items allow students to employ different solution strategies, whereas science items offer fewer degrees of freedom for test takers (Nentwig et al. [2009]). In particular, the shared format of items in math, science, and problem solving may explain an overlap between their cognitive demands. For instance, most of the items were designed in such a way that students had to extract and identify relevant information from given tables or figures in order to solve specific problems. Hence, these items were static and did not require knowledge generation by interaction or exploration but rather the use of given information in problem situations (Wood et al. [2009]). In contrast to the domain-specific items in math and science, problem solving items did not require the use of prior knowledge in math and science (OECD [2004]). In addition, some of the math and science items involved cognitive operations that were specific to these domains. For instance, students had to solve a number of math items by applying arithmetic and combinatorial operations (OECD [2005]). Finally, since items referred to contextual stimuli, which were presented in textual formats, reading ability can be regarded as another, shared demand of solving the items. Furthermore, Rindermann ([2007]) clearly showed that the shared demands of the achievement tests in large-scale assessments such as PISA were strongly related to students’ general reasoning skills. This finding is in line with the strong relations between math, science, and problem solving competence, found in our study. The interpretation of the overlap between the three competences can also be interpreted from a conceptual point of view. In light of the competence frameworks in PISA, we argue that there are a number of skills that can be found in math, science, and problem solving: information retrieval and processing, knowledge application, and evaluation of results (Griffin et al. [2012]; OECD [2004], [2005]). These skills point out to the importance of reasoning in the three domains (Rindermann [2007]). Thus, the empirical overlap between math and problem solving can be explained by shared processes of, what Mayer ([2010]) refers to as, informal reasoning. On the other hand, the stronger effect of math competence could be an effect of the quality of math education. Hiebert et al. ([1996]) and Kuo et al. ([2013]) suggested that math education is more based on problem solving skills than other subjects in school (e.g., Polya [1945]). Science lessons, in contrast, are often not necessarily problem-based, despite the fact that they often start with a set problem. Risch ([2010]) showed in a cross-national review that science learning was more related to contents and contexts rather than to generic problem-solving skills. These tendencies might lead to a weaker contribution of science education to the development of problem solving competence (Abd-El-Khalick et al. [2004]).
In sum, we found support on the Moderation-Hypothesis, which assumed systematic differences in the contribution of math and science competence to problem solving competence across the 41 PISA 2003 countries.
The concept of math-science coherence
The relation to problem solving
In our study, we introduced the concept of math-science coherence, which reflects the degree to which math and science education are harmonized. Since mathematical and scientific literacy show a conceptual overlap, which refers to a set of cognitive processes that are linked to reasoning and information processing (Fensham and Bellocchi [2013]; Mayer [2010]), a significant relation between math-science coherence and problem solving was expected. In our analyses, we found a significant and positive effect of math-science coherence on performance scores in problem solving. In this finding we see evidence for the validity of this newly introduced concept of math-science coherence and its focus on the synergistic effect of math and science education on problem solving. The results further suggest that higher levels of coordination between math and science education has beneficial effects on the development of cross-curricular problem-solving competence (as measured within the PISA framework).
Confounding effects of country characteristics
As another step of validating the concept of math-science coherence, we investigated whether country-specific characteristics that are linked to society-, curriculum-, and school-related factors confounded its relation to problem solving. Our results showed that national intelligence, the Human Development Index, the integration of the science curriculum, and schools’ autonomy were positively linked to math-science coherence and problem solving, whilst a schools’ frequency of assessment had a negative confounding effect.
The findings regarding the positive confounders are in line with and also extend a number of studies on cross-country differences in education (e.g., Blömeke et al. [2011]; Dronkers et al. [2014]; Janssen and Geiser [2012]; Risch [2010]). Ross and Hogaboam-Gray ([1998]), for instance, found that students benefit from an integrated curriculum, particularly in terms of motivation and the development of their abilities. In the context of our confounder analysis, the integration of the science curriculum as well as the autonomy to allocate resources is expected to positively affect math-science coherence. At the same time, an integrated science curriculum with a coordinated allocation of resources may promote inquiry-based experiments in science courses, which is assumed to be beneficial for the development of problem solving within and across domains. Teaching science as an integrated subject is often regarded a challenge for teachers, particularly when developing conceptual structures in science lessons (Lang and Olson, [2000]), leading to teaching practices in which cross-curricular competence is rarely taken into account (Mansour [2013]; van Merriënboer [2013]).
The negative confounding effect of assessment frequency suggests that high frequencies of assessment, as it presumably applies to both math and science subjects, contribute positively to math-science coherence. However, the intended or unintended engagement in educational activities associated with assessment preparation tends not to be conducive to effectively developing domain-general problem solving competence (see also Neumann et al. [2012]).
The positive confounder effect of HDI is not surprising as HDI reflects a country’s capability to distribute resources and to enable certain levels of autonomy (Reich et al. [2013]). To find national intelligence as a positive confounder is also to be expected as the basis for its estimation are often students’ educational outcome measures (e.g., Rindermann [2008]) and, as discussed earlier, academic achievement measures share the involvement of a set of cognitive processes (Baumert et al. [2009]; OECD [2004]).
In summary, the synergistic effect of a coherent math and science education on the development of problem solving competence is substantially linked to characteristics of a country’s educational system with respect to curricula and school organization in the context of its socio-economic capabilities. Math-science coherence, however, also is linked to the extent to which math or science education is able to utilise students’ educational capabilities.
Math-science coherence and capability-utilisation
So far, discrepancies between students’ performance in math and problem solving or science and problem solving have been discussed as indicators of students’ capability utilisation in math or science (Leutner et al. [2012]; OECD [2004]). We have extended this perspective by introducing Capability Under-Utilisation Indices for math and science to investigate the effectiveness with which knowledge and skills acquired in the context of math or science education are transferred into cross-curricular problem-solving competence. The Capability Under-Utilisation Indices for math and science reflect a potential quantitative imbalance between math, science, and problem solving performance within a country, whilst the also introduced concept of math-science coherence reflects a potential qualitative imbalance between math and science education.
The results of our analyses suggest that an under-utilisation of problem solving capabilities in the acquisition of science literacy is linked to lower levels of math-science coherence, which ultimately leads to lower scores in problem solving competence. This interpretation finds resonance in Ross and Hogaboam-Gray’s ([1998]) argumentation for integrating math and science education and supports the attempts of math and science educators to incorporate higher-order thinking skills in teaching STEM subjects (e.g., Gallagher et al. [2012]; Zohar [2013]).
In contrast, the CUU Index for math was not related to math-science coherence in our analyses. This might be due to the conceptualizations and assessments of mathematical literacy and problem solving competence. Both constructs share cognitive processes of reasoning and information processing, resulting in quite similar items. Consequently, the transfer from math-related knowledge and skills to cross-curricular problems does not necessarily depend on how math and science education are harmonised, since the conceptual and operational discrepancy between math and problem solving is rather small.
Conclusions
Math and science education do matter to the development of students’ problem-solving skills. This argumentation is based on the assumption that the PISA assessments in math, science, and problem solving are able to measure students’ competence as outcomes, which are directly linked to their education (Bulle [2011]; Kind [2013]). In contrast to math and science competence, problem solving competence is not explicitly taught as a subject. Problem solving competence requires the utilisation of knowledge and reasoning skills acquired in specific domains (Pellegrino and Hilton [2012]). In agreement with Kuhn ([2009]), we point out that this transfer does not happen automatically but needs to be actively facilitated. In fact, Mayer and Wittrock ([2006]) stressed that the development of transferable skills such as problem solving competence needs to be fostered within specific domains rather than taught in dedicated, distinct courses. Moreover, they suggested that students should develop a “repertoire of cognitive and metacognitive strategies that can be applied in specific problem-solving situations” (p. 299). Beyond this domain-specific teaching principle, research also proposes to train the transfer of problem solving competence in domains that are closely related (e.g., math and science; Pellegrino and Hilton [2012]). In light of the effects of aligned curricula (as represented by the concept of math-science coherence), we argue that educational efforts to increase students’ problem solving competence may focus on a coordinated improvement of math and science literacy and fostering problem solving competence within math and science. The emphasis is on coordinated, as the results of our analyses indicated that the coherence between math and science education, as a qualitative characteristic of a country’s educational system, is a strong predictor of problem solving competence. This harmonisation of math and science education may be achieved by better enabling the utilisation of capabilities, especially in science education. Sufficiently high levels of math-science coherence could facilitate the emergence of educational synergisms, which positively affect the development of problem solving competence. In other words, we argue for quantitative changes (i.e., improve science attainment) in order to achieve qualitative changes (i.e., higher levels of curriculum coherence), which are expected to create effective transitions of subject-specific knowledge and skills into subject-unspecific competences to solve real-life problems (Pellegrino and Hilton [2012]; van Merriënboer [2013]).
Finally, we encourage research that is concerned with the validation of the proposed indices for different forms of problem solving. In particular, we suggest studying the facilities of the capability-under-utilisation indices for analytical and dynamic problem solving, as assessed in the PISA 2012 study (OECD [2014]). Due to the different cognitive demands in analytical and dynamic problems (e.g., using existing knowledge vs. generating knowledge; OECD [2014]), we suspect differences in capability utilisation in math and science. This research could provide further insights into the role of 21st century skills as educational goals.
Footnotes
aThe differences between students’ achievement in mathematics and problem solving, and science and problem solving have to be interpreted relative to the OECD average, since the achievement scales were scaled with a mean of 500 and a standard deviation of 100 for the OECD countries (OECD [2004], p. 55). Although alternative indices such as country residuals may also be used in cross-country comparisons (e.g., Olsen [2005]), we decided to use CUU indices, as they reflect the actual differences in achievement scores.
bIn addition, we checked whether this result was due to the restricted variances in low-performing countries and found that neither ceiling nor floor effects in the problem solving scores existed. The problem solving scale differentiated sufficiently reliably in the regions below and above the OECD mean of 500.
References
Abd-El-Khalick F, Boujaoude S, Duschl R, Lederman NG, Mamlok-Naaman R, Hofstein A, Niaz M, Treagust D, Tuan H-L: Inquiry in science education: International perspectives. Science Education 2004, 88: 397–419. doi:10.1002/sce.10118 10.1002/sce.10118
Adams RJ: Reliability as a measurement design effect. Studies in Educational Evaluation 2005, 31: 162–172. doi:10.1016/j.stueduc.2005.05.008 10.1016/j.stueduc.2005.05.008
Arts J, Gijselaers W, Boshuizen H: Understanding managerial problem solving, knowledge use and information processing: Investigating stages from school to the workplace. Contemporary Educational Psychology 2006, 31: 387–410. doi:10.1016/j.cedpsych.2006.05.005 10.1016/j.cedpsych.2006.05.005
Bassok M, Holyoak K: Pragmatic knowledge and conceptual structure: determinants of transfer between quantitative domains. In Transfer on trial: intelligence, cognition, and instruction. Edited by: Detterman DK, Sternberg RJ. Ablex, Norwood, NJ; 1993:68–98.
Baumert J, Lüdtke O, Trautwein U, Brunner M: Large-scale student assessment studies measure the results of processes of knowledge acquisition: evidence in support of the distinction between intelligence and student achievement. Educational Research Review 2009, 4: 165–176. doi:10.1016/j.edurev.2009.04.002 10.1016/j.edurev.2009.04.002
Beckmann JF: Zur Validierung des Konstrukts des intellektuellen Veränderungspotentials [On the validation of the construct of intellectual change potential]. logos, Berlin; 2001.
Blömeke S, Houang R, Suhl U: TEDS-M: diagnosing teacher knowledge by applying multidimensional item response theory and multiple-group models. IERI Monograph Series: Issues and Methodologies in Large-Scale Assessments 2011, 4: 109–129.
Bouhilila D, Sellaouti F: Multiple imputation using chained equations for missing data in TIMSS: a case study. Large-scale Assessments in Education 2013, 1: 4.
Brunner M, Gogol K, Sonnleitner P, Keller U, Krauss S, Preckel F: Gender differences in the mean level, variability, and profile shape of student achievement: Results from 41 countries. Intelligence 2013, 41: 378–395. doi:10.1016/j.intell.2013.05.009 10.1016/j.intell.2013.05.009
Bulle N: Comparing OECD educational models through the prism of PISA. Comparative Education 2011, 47: 503–521. doi: 10.1080/03050068.2011.555117 10.1080/03050068.2011.555117
Bybee R: Scientific Inquiry and Science Teaching. In Scientific Inquiry and the Nature of Science. Edited by: Flick L, Lederman N. Springer & Kluwers, New York, NY; 2004:1–14. doi:10.1007/978–1-4020–5814–1_1
Chiu M, Chow B: Classroom discipline across forty-One countries: school, economic, and cultural differences. Journal of Cross-Cultural Psychology 2011, 42: 516–533. doi:10.1177/0022022110381115 10.1177/0022022110381115
Drake S, Reid J: Integrated curriculum: Increasing relevance while maintaining accountability. Research into Practice 2010, 28: 1–4.
Dronkers J, Levels M, de Heus M: Migrant pupils’ scientific performance: the influence of educational system features of origin and destination countries. Large-scale Assessments in Education 2014, 2: 3.
Enders C: Applied Missing Data Analysis. The Guilford Press, New York, NY; 2010.
Ewell P: A world of assessment: OECD’s AHELO initiative. Change: The Magazine of Higher Learning 2012, 44: 35–42. doi:10.1080/00091383.2012.706515 10.1080/00091383.2012.706515
Fensham P, Bellocchi A: Higher order thinking in chemistry curriculum and its assessment. Thinking Skills and Creativity 2013, 10: 250–264. doi:10.1016/j.tsc.2013.06.003 10.1016/j.tsc.2013.06.003
Gallagher C, Hipkins R, Zohar A: Positioning thinking within national curriculum and assessment systems: perspectives from Israel, New Zealand and Northern Ireland. Thinking Skills and Creativity 2012, 7: 134–143. doi:10.1016/j.tsc.2012.04.005 10.1016/j.tsc.2012.04.005
Greiff S, Holt D, Funke J: Perspectives on problem solving in educational assessment: analytical, interactive, and collaborative problem solving. The Journal of Problem Solving 2013, 5: 71–91. doi:10.7771/1932–6246.1153 10.7771/1932-6246.1153
Griffin P, Care E, McGaw B: The changing role of education and schools. In Assessment and Teaching of 21st Century Skills. Edited by: Griffin P, McGaw B, Care E. Springer, Dordrecht; 2012:1–15. 10.1007/978-94-007-2324-5_1
Hickendorff M: The language factor in elementary mathematics assessments: Computational skills and applied problem solving in a multidimensional IRT framework. Applied Measurement in Education 2013, 26: 253–278. doi:10.1080/08957347.2013.824451 10.1080/08957347.2013.824451
Hiebert J, Carpenter T, Fennema E, Fuson K, Human P, Murray H, Olivier A, Wearne D: Problem Solving as a Basis for Reform in Curriculum and Instruction: The Case of Mathematics. Educational Researcher 1996, 25: 12–21. doi:10.3102/0013189X025004012 10.3102/0013189X025004012
Holliday W, Holliday B: Why using international comparative math and science achievement data from TIMSS is not helpful. The Educational Forum 2003, 67: 250–257. 10.1080/00131720309335038
Hox J: Multilevel Analysis. 2nd edition. Routlegde, New York, NY; 2010.
Janssen A, Geiser C: Cross-cultural differences in spatial abilities and solution strategies: An investigation in Cambodia and Germany. Journal of Cross-Cultural Psychology 2012, 43: 533–557. doi:10.1177/0022022111399646 10.1177/0022022111399646
Jonassen D: Learning to solve problems. Routledge, New York, NY; 2011.
Kind P: Establishing Assessment Scales Using a Novel Disciplinary Rationale for Scientific Reasoning. Journal of Research in Science Teaching 2013, 50: 530–560. doi:10.1002/tea.21086 10.1002/tea.21086
Klahr D, Dunbar K: Dual Space Search during Scientific Reasoning. Cognitive Science 1988, 12: 1–48. doi:10.1207/s15516709cog1201_1 10.1207/s15516709cog1201_1
Koeppen K, Hartig J, Klieme E, Leutner D: Current issues in competence modeling and assessment. Journal of Psychology 2008, 216: 61–73. doi:10.1027/0044–3409.216.2.61
Kuhn D: Do students need to be taught how to reason? Educational Research Review 2009, 4: 1–6. doi:10.1016/j.edurev.2008.11.001 10.1016/j.edurev.2008.11.001
Kuo E, Hull M, Gupta A, Elby A: How Students Blend Conceptual and Formal Mathematical Reasoning in Solving Physics Problems. Science Education 2013, 97: 32–57. doi:10.1002/sce.21043 10.1002/sce.21043
Lang M, Olson J: Integrated science teaching as a challenge for teachers to develop new conceptual structures. Research in Science Education 2000, 30: 213–224. doi:10.1007/BF02461629 10.1007/BF02461629
Leutner D, Fleischer J, Wirth J, Greiff S, Funke J: Analytische und dynamische Problemlösekompetenz im Lichte internationaler Schulleistungsstudien [Analytical and dynamic problem-solvng competence in international large-scale studies]. Psychologische Rundschau 2012, 63: 34–42. doi:10.1026/0033–3042/a000108 10.1026/0033-3042/a000108
Lynn R, Meisenberg G: National IQs calculated and validated for 108 nations. Intelligence 2010, 38: 353–360. doi:10.1016/j.intell.2010.04.007 10.1016/j.intell.2010.04.007
MacKinnon D, Krull J, Lockwood C: Equivalence of the mediation, confounding, and suppression effect. Prevention Science 2000, 1: 173–181. doi:10.1023/A:1026595011371 10.1023/A:1026595011371
Mansour N: Consistencies and inconsistencies between science teachers’ beliefs and practices. International Journal of Science Education 2013, 35: 1230–1275. doi:10.1080/09500693.2012.743196 10.1080/09500693.2012.743196
Martin M, Mullis I, Gonzalez E, Chrostowski S: TIMSS 2003 International Science Report. IEA, Chestnut Hill, MA; 2004.
Martin AJ, Liem GAD, Mok MMC, Xu J: Problem solving and immigrant student mathematics and science achievement: Multination findings from the Programme for International Student Assessment (PISA). Journal of Educational Psychology 2012, 104: 1054–1073. doi:10.1037/a0029152 10.1037/a0029152
Mayer R: Problem solving and reasoning. In International Encyclopedia of Education. 3rd edition. Edited by: Peterson P, Baker E, McGraw B. Elsevier, Oxford; 2010:273–278. doi:10.1016/B978–0-08–044894–7.00487–5 10.1016/B978-0-08-044894-7.00487-5
Mayer R, Wittrock MC: Problem solving. In Handbook of Educational Psychology. 2nd edition. Edited by: Alexander PA, Winne PH. Lawrence Erlbaum, New Jersey; 2006:287–303.
Muthén B, Muthén L: Mplus 6. Muthén & Muthén, Los Angeles, CA; 2010.
Successful K-12 STEM Education. National Academies Press, Washington, DC; 2011.
Nentwig P, Rönnebeck S, Schöps K, Rumann S, Carstensen C: Performance and levels of contextualization in a selection of OECD countries in PISA 2006. Journal of Research in Science Teaching 2009, 8: 897–908. doi:10.1002/tea.20338 10.1002/tea.20338
Neumann K, Kauertz A, Fischer H: Quality of Instruction in Science Education. In Second International Handbook of Science Education (Part One. Edited by: Fraser B, Tobin K, McRobbie C. Springer, Dordrecht; 2012:247–258.
The PISA 2003 Assessment Frameworks. OECD, Paris; 2003.
Problem solving for tomorrow’s world. OECD, Paris; 2004.
PISA 2003 Technical Report. OECD, Paris; 2005.
PISA 2012 Results : Creative Problem Solving – Students’ Skills in Tackling Real-Life Problems (Vol. V). OECD, Paris; 2014.
Olsen RV: An exploration of cluster structure in scientific literacy in PISA: Evidence for a Nordic dimension? NorDiNa. ᅟ 2005, 1(1):81–94.
Oser F, Baeriswyl F: Choreographies of Teaching: Bridging Instruction to Learning. In Handbook of Research on Teaching. 4th edition. Edited by: Richardson V. American Educational Research Association, Washington, DC; 2001:1031–1065.
Pellegrino JW, Hilton ML: Education for Life and Work – Developing Transferable Knowledge and Skills in the 21st Century. The National Academies Press, Washington, DC; 2012.
Polya G: How to solve it: a new aspect of mathematical method. Princeton University Press, Princeton, NJ; 1945.
Reich J, Hein S, Krivulskaya S, Hart L, Gumkowski N, Grigorenko E: Associations between household responsibilities and academic competencies in the context of education accessibility in Zambia. Learning and Individual Differences 2013, 27: 250–257. doi:10.1016/j.lindif.2013.02.005 10.1016/j.lindif.2013.02.005
Rindermann H: The g-factor of international cognitive ability comparisons: The homogeneity of results in PISA, TIMSS, PIRLS and IQ-tests across nations. European Journal of Personality 2007, 21: 661–706. doi:10.1002/per.634
Rindermann H: Relevance of education and intelligence at the national level for the economic welfare of people. Intelligence 2008, 36: 127–142. doi:10.1016/j.intell.2007.02.002 10.1016/j.intell.2007.02.002
Risch B: Teaching Chemistry around the World. Waxmann, Münster; 2010.
Ross J, Hogaboam-Gray A: Integrating mathematics, science, and technology: effects on students. International Journal of Science Education 1998, 20: 1119–1135. doi:10.1080/0950069980200908 10.1080/0950069980200908
Snijders TAB, Bosker RJ: Multilevel Analysis: An Introduction to Basic and Advanced Multilevel Modeling. 2nd edition. Sage Publications, London; 2012.
Human Development Report 2005. UNDP, New York, NY; 2005.
Van Merriënboer J: Perspectives on problem solving and instruction. Computers & Education 2013, 64: 153–160. doi:10.1016/j.compedu.2012.11.025 10.1016/j.compedu.2012.11.025
Wood RE, Beckmann JF, Birney D: Simulations, learning and real world capabilities. Education Training 2009, 51(5/6):491–510. doi:10.1108/00400910910987273 10.1108/00400910910987273
Wu M: The role of plausible values in large-scale surveys. Studies in Educational Evaluation 2005, 31: 114–128. doi:10.1016/j.stueduc.2005.05.005 10.1016/j.stueduc.2005.05.005
Wu M, Adams R: Modelling Mathematics Problem Solving Item Responses using a Multidimensional IRT Model. Mathematics Education Research Journal 2006, 18: 93–113. doi:10.1007/BF03217438 10.1007/BF03217438
Wüstenberg S, Greiff S, Funke J: Complex problem solving: More than reasoning? Intelligence 2012, 40: 1–14. doi:10.1016/j.intell.2011.11.003 10.1016/j.intell.2011.11.003
Zohar A: Scaling up higher order thinking in science classrooms: the challenge of bridging the gap between theory, policy and practice. Thinking Skills and Creativity 2013, 10: 168–172. doi:10.1016/j.tsc.2013.08.001 10.1016/j.tsc.2013.08.001
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
RS carried out the analyses, participated in the development of the rationale, and drafted the manuscript. JFB carried out some additional analyses, participated in the development of the rationale, and drafted the manuscript. Both authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Scherer, R., Beckmann, J.F. The acquisition of problem solving competence: evidence from 41 countries that math and science education matters. Large-scale Assess Educ 2, 10 (2014). https://doi.org/10.1186/s40536-014-0010-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40536-014-0010-7